Math Minds
A professional community dedicated to
the effective teaching of K-12 mathematics
What is Math Minds?
The Math Minds approach is neither traditional nor reform as those terms are commonly understood. While traditional approaches offer much-needed structure, and reform approaches highlight the importance of sense-making, it can be difficult to structure sense-making in a way that supports all learners in engaging with conceptually sound mathematical ideas. For those with gaps in their understanding, finding a suitable entry point is key, and providing meaningful opportunities for extension and further learning is essential for all. Math Minds offers practical ways to make this happen.
What does Math Minds offer?




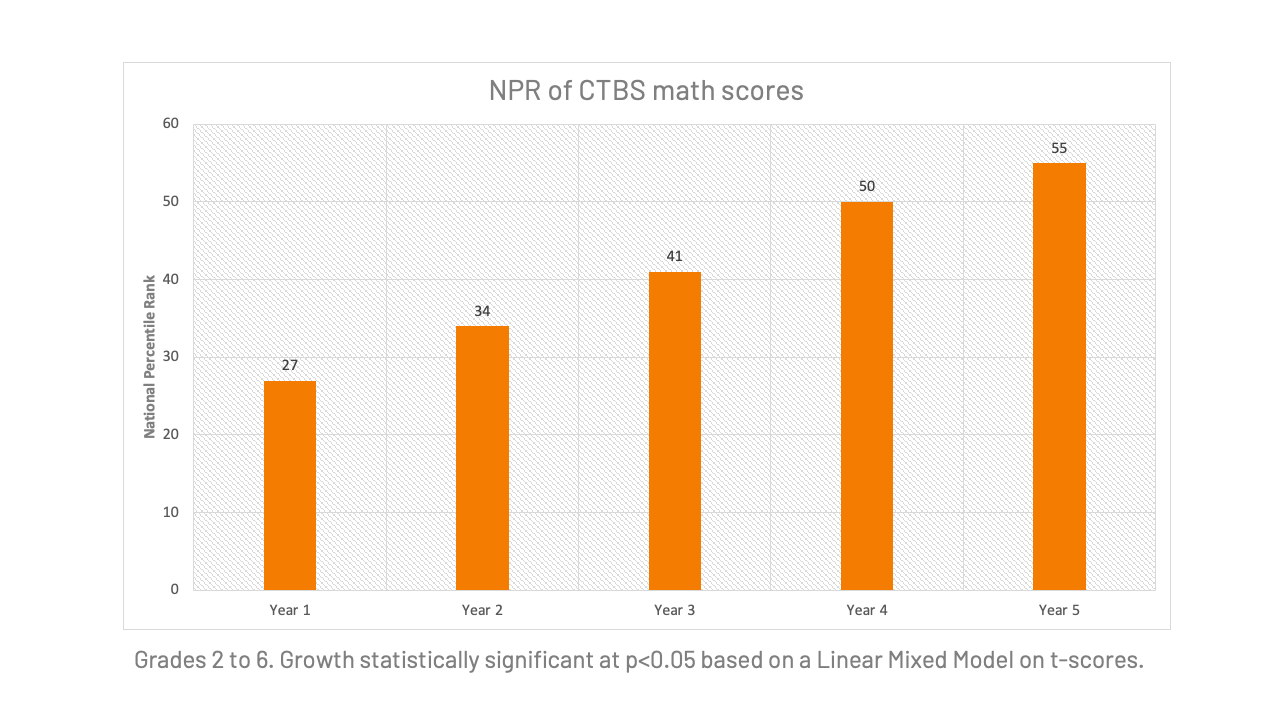
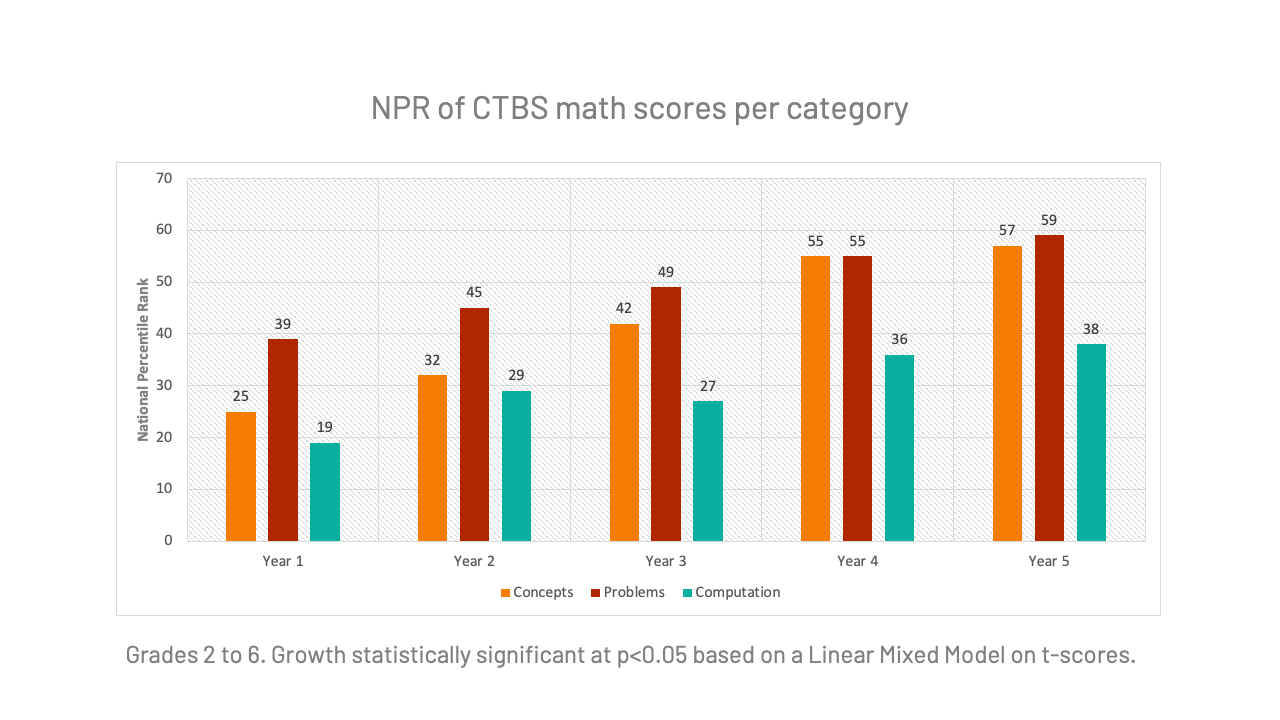
What is the evidence supporting our approach?
Please further note that these data represent year-over-year improvements. Learners don’t experience a one-time boost in achievement. They continue to accelerate as they experience this manner of teaching.
For more information on our publications, please click on the button below to visit the Math Minds Online Community.
What makes this course unique?
This course aims to provide a user’s introduction to a coherent, theory-rich, evidence-based approach to teaching mathematics. While the principles we present in the course apply to all levels, the majority of the examples and illustrations we offer are derived from elementary level mathematics.
Unit 1
Available now
Unit 2
Available now
Unit 3
Available now
What to Expect from The Course
The course offers advice on assessing and selecting classroom resources.
The course offers support when using those resources to choose, adapt, and craft tasks that are suited to your students.
The course provides strategies for gathering feedback from learners and using that feedback.
What Not to Expect
Our research has shown that it takes concentrated and sustained effort to become adept at using the model.
The course is designed to interrupt deep-seated habits that were developed as a student and reinforced by teaching.
The Math Minds model is committed to integrating contemporary research on learning; we don’t offer any sort of stand-alone advice on popular trends.
Testimonials
I really liked that there were so many interactive activities. It forced me to look at things from a different perspective, not just as a teacher but in the mindset of what a student might do.
AmandaGrade 1 Teacher, Canada
So far, this course has really made me aware of the language I am using while teaching and having conversations with my students.
MonicaGrade 1 teacher, Canada
This course has helped me to look at my own teaching practices and made me more aware of how I am teaching these critical discernments - the emphasis of realizing it’s not just about the steps, but how the thinking behind the steps is crucial.
ShailaGrade 4 teacher, Canada
Not easier work at all—in my older way of thinking, it was making sure that students had so many different ways to engage in the math at their level. With the RaPID model, you could teach the one lesson and still engage everyone at the level that’s needed for them.
PeterGrade 5 Teacher, Canada
I really found the Number Talk section to be a real highlight. Because that’s kind of a buzzword. Lots of people use Number Talks. And to really think critically about how we use Number Talks—and look through the lens of the RaPID model—was very, very valuable. I used Number Talks in my Grade Six Math class, and I started really thinking more critically about how I’m doing it, and I’ve been doing some in my Google Meets and being very intentional now since looking at this and changing it up a bit a result of this particular section. I appreciated that. I had not thought about it that way before.
MichelleAssociate Principal and Grade 6 teacher, Canada
After completing the first unit of Math Minds, I now have a new conceptual understanding of how I can enable/support my diversity of learners to make conceptual understandings themselves; e.g., not thinking multi-digit multiplication is a step by step process but instead a process of identifying relationships between numbers working together.